|
| Main Page | Philoman's Question Archive | Philoman's Theorems |
| Suggested Sites | Cool Facts | Cool Words |
| Jokes | Quotes | Tips for Internet & Windows |
***
|
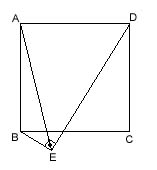
|AB|=|AC|, |BC|=|AD|, m(ABC)=50, m(BAD)=90;
m(ADC)=? ---- Let E be point in the exterior region of ABC such that m(ABE)=60 and |BE|=|AB|. Then ABE is an equilateral triangle and AEC is an isosceles triangle where |AE|=|AC|. So, m(AEC)=80. Looking carefully, we see that CBE and DAC are congruent triangles (by side angle side rule; |AD|=|BC|, m(DAC)=m(CBE), |AC|=|BE|). Therefore m(ADC)=m(BCE)=30. One of Philoman's theorems could be used in this question and some other questions that satisfy the same conditions. Click here to see the theorem. |
|
*** (Back to Top)
 |
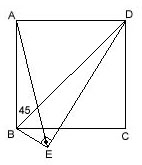
ABCD is a square, m(BED)=90; m(AED)=? ---- Draw diagonal of the square (BD) and m(ABD)=45. Since m(BAD)+m(BED)=180, those four points (A,B,D,E) could be located on a circle. Then as ABD and AED are seeing the same arc, m(ABD)=m(AED)=45. |
 |
*** (Back to Top)
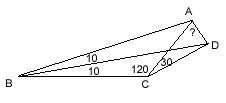 |
m(ABD)=m(DBC)=10,
m(ACB)=120, m(ACD)=30; m(CAD)=? ---- |BD| is an interior angle bisector as given in the question. Since m(DCF)=30, |CD| is an exterior angle bisector. As |BD|, |CD| and |AD| intersect at the same point and |BD| and |CD| are angle bisectors then |AD| has to be an exterior angle bisector as well. Using this, m(CAD)=70. |
 |
*** (Back to Top)
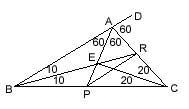
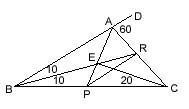 |
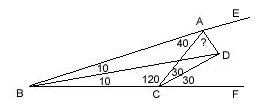
m(DAC)=60,
m(DBR)=m(RBC)=10, m(ECP)=20; m(RPC)=? ---- m(RCE)=20. |BE| and |CE| are angle bisectors, so, |AE| is also an angle bisector. m(BAP)=m(PAC)=60. |BR| and |AR| are angle bisectors, so, |PR| is also an angle bisector. Then, m(RPC)=40. |
 |
*** (Back to Top)
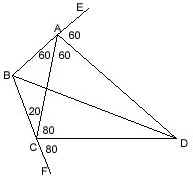
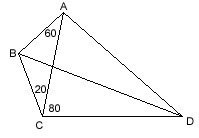 |
m(BAC)=60,
m(BCA)=20, m(ACD)=80, m(ADC)=40; m(ABD)=? ---- Extend |BA| and |BC|. Then it is clear that |AD| and |CD| are exterior angle bisectors of the triangle ABC. So, |BD| must be an interior angle bisector as they all intersect at point D. Therefore, m(ABD)=50. |
 |
*** (Back to Top)
Suppose these two conditions: You are given an angle of 19 degrees on a plane and you are asked to construct an angle of 1 degree by using only compasses; you are given an angle of 17 degrees on a plane and you are asked to construct an angle of 3 degrees by using only compasses. How would you do these? (Hint: Both are done using the same way)
----
Suppose it is m(ABC)=19 is given to you. Draw a circle with center B and make sure the circle intersects with the sides of the angle. Let's name the points that the circle intersects with: D and E. Place tips of the compasses on D and E. Then using that, measure another 19 degrees on the circle. If you do this 19 times, then you will get 19*19=361 degrees. I think you understood where that 1 degree is constructed. You completed the circle and the small arc that exceeds measures 1 degree.
Using the same way, you could do the other exercise. Just to remind 17*21=357; the remaining arc to complete the circle will measure 3 degrees.
*** (Back to Top)
Assume that you are given lengths of 7 and 24 units on a plane. How would you draw a 25 units long line using compasses and a ruler (which you are not allowed to use to measure lengths of course :))?
----
Since 7*7+24*24=25*25, there is a right triangle with the sides 7, 24 and 25. Then the question changes into building a right angle rather than drawing a length of 25 units. Using the compasses construct two isosceles triangles (ABC and ABD) with a common base (|AB|) and then draw |CD| with the help of yur ruler. Here |CD| is perpendicular to |AB|. The next thing to do is carry 7 and 24 units to the sides of this right angle using the compasses. The hypotenuse of the right triangle you constructed will equal 25 units in length.
*** (Back to Top)
1, 8, 29, 70, 137, ?
Which number comes next?
----
8 - 1 = 7
29 - 8 = 21
70 - 29 = 41
137 - 70 = 67
21 - 7 = 14
41 - 21 = 20
67 - 41 = 26
In the first group of numbers you see the difference between the elements of the series. In the second group you see the differences between the results of the first group. You see that the difference between the results of the second group is always 6. Then, to find the next number, we must add 6 to 26, which makes 32; and then and 32 to 67 to find 99; and then finally add 99 to 137 to find the answer 236.
This serie was an easy one but here is another method that uses one of Philoman's Theorems. It could be applied in more difficult situations. Click here to see the theorem.
To find the next number using this method first we must find a relationship between the elements of the series. Let's try:
8 ¹ 1
29 ¹ 2*8 - 1
70 ¹ 3*29 - 3*8 + 1
137 = 4*70 - 6*29 + 4*8 - 1 (Bingo, we found it!)
The only thing we are to do now is, apply the same relationship to find the next number:
? = 4*137 - 6*70 + 4*29 - 8 = 236. You see, it is the same result. Check the calculations if you like.
We found the relationship we looked for on the fourth step. That means the function that could be used to construct this series is of the third degree. You could write the general formula of third degree function and after solving an equation system with four unknowns you can calculate the function itself. If you would like to do it, do it; if you don't check if this one works ;)) :
f(x) = x³ + x² - 3x + 2 (see that f(1) = 1, f(2) = 8, f(3) = 29, f(4) = 70, f(5) = 137, f(6) = 236 etc.)
There is another thing left to say: If you can't find a relationship between the given elements of the series, then you cannot calculate the function which created the serie either because the serie was not created using a function or the d[f(x)] > number of given elements - 2 (in other words you need more elements of the serie in order to calculate the function).
Try this method with some other examples (simple ones for the beginning) and you'll see that it works all the time.
*** (Back to Top)
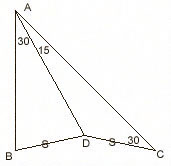 |
m(BAD)=30,
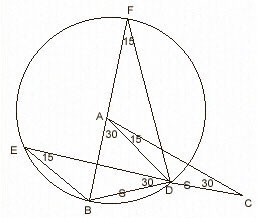
m(DAC)=15, m(DCA)=30 and |BD|=|DC|; m(ABD)=? ---- Take point E where m(BDE)=30 and |DE|=|AC|. EDB and ACD are congruent triangles. So, m(BED)=15. Now draw the circle that passes from E, B and D (any three non-collinear points determine a circle). Extend |AB| and let it cut the circle at point F. If you draw |FD|, you see that m(BED)=m(BFD)=15. Since m(BFD)+m(ADF)=m(BAD)=30, m(ADF) is also 15. Then, |AF|=|AD|. Using this one, we can conclude that A is the center of the circle. As A is the center, |AB|=|AD| and this gives m(ABD)=75. |
 |
*** (Back to Top)
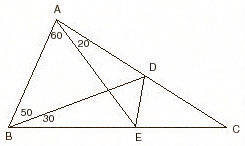 |
m(ABD)=50,
m(BAE)=60, m(EAD)=20, m(EBD)=30; m(BDE)=? ---- Get a point F on |BC| which satisfies m(BAF)=20; from this, m(FAE)=40. |BA|=|AF| because BAF is an isosceles triangle. Also BAD is an isosceles triangle and |BA|=|AD|. From here |AF|=|AD| and since m(FAD)=60, FAD is an equilateral triangle. After putting in the values of the angles you can see that m(BDE)=10 and m(AEF)=40. As m(AEF)=m(EAF), AFE is an isosceles triangle; |AF|=|FE|. From here |DF|=|FE| and since m(DFE)=40, m(FDE)=70. m(BDE)=m(BDF)+m(FDE). So, m(BDE)=80. |
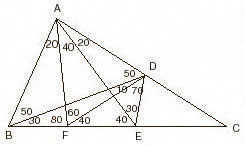 |