|
| Main Page | Philoman's Question Archive | Philoman's Theorems |
| Suggested Sites | Cool Facts | Cool Words |
| Jokes | Quotes | Tips for Internet & Windows |
Philoman's Question Archive new (1-10) (11-20) (21-29) |
||
***
n0 is equal to 1 for all non-zero values of n. Why is 00 undefined?
----
We know that am-n is equal to am/an. Since a0 can be written as an-n and an-n is equal to an/an, a0 is equal to 1 with only one exception. That exception rises from the point that an cannot be equal to 0; because if it does, an/an would be undefined. an is equal to zero only when a is equal to zero. So, that is when an is undefined.
*** (Back to Top)
Two cities P and R are 100 km apart. A car starts travelling from P to R with a velocity of 60 km/h and another car starts travelling from R to P with a velocity of 40 km/h at the same instant. Again at the same instant a bird flying a constant 80 km/h passes over the first car and heads for city R. When the bird meets the second car on its way, it turns back and starts going for city P. It again changes its route when it meets the first car. The bird flies between the cars like a bouncing ball until the cars meet. How many kilometers would the bird fly in this trip?
----
The cars would meet in an hour since they travel with constant speeds of 60 km/h and 40 km/h with an initial distance of 100 km. Using this information, we can conclude that the bird also flies for an hour between the cars (until the cars meet) thus flying a distance of 80 km.
*** (Back to Top)
Find all points of the xy plane which are equidistant from the x-axis, the y-axis and the point (3,6).
----
A point which is equidistant from both the x-axis and the y-axis must have the same abcissa and ordinate which can be denoted by (k,k) (in other words, this point is on the line x - y = 0). We now write the distance between (3,6) and (k,k) which must equal "k" according to the question:
(3 - k)2 - (6 - k)2 = k2
Solving for k in this equation we get k=3 or k=15. So, (3,3) and (15,15) are the points which satisfy the given conditions.
*** (Back to Top)
Show that if a > 0, then a + (1/a) ³ 2.
----
We know that a > 0 and (a-1)2 ³ 0. Then; (a-1)2/a ³ 0. If you evaluate the expression on the right side you get (a2 - 2a + 1)/a ³ 0. That simplifies to
a - 2 + (1/a) ³ 0
which is equivalent to the inequality we are looking for.
*** (Back to Top)
Show that if a > 0, then Ö(a+1) - Öa < 1/Ö(a+1)
----
Since a > 0, a2 + a > a2. Using this, a(a+1) > a2 or in other words a > a2/(a+1). Taking square root of both sides, we obtain Öa > a/Ö(a+1). If you rewrite this like Öa > (a+1-1)/Ö(a+1) and write the right side as the sum of two fractions you get
Öa > (a+1)/Ö(a+1) - 1/Ö(a+1)
which then simplifies to
Öa > Ö(a+1) - 1/Ö(a+1).
Rearranging this inequality you can get the inequality we have been trying to prove.
*** (Back to Top)
|
Formulate a way to find the
area of a regular polygon with n sides and perimeter P. ---- Let the three sides in the shape be any consecutive three sides of a regular polygon. O is the center of both the inscribed circle and the circumcircle. Because of that, AOB is an isosceles triangle. OH is the radius of the inscribed circle and also height of AOB which is perpendicular to the base. Since perimeter of the regular polygon is P, |AB| is equal to P/n and |AH|=|HB|=P/2n. Also, m(AOB)=360/n and m(AOH)=m(HOB)=360/2n=180/n. |OH|=r. Using this information we conclude that tan(180/n)=(P/2n)/r=P/2nr. Calculating for r we get, r=P/(2n*tan(180/n)). Now, we are going to use the formula A=u*r to calculate the area of the regular polygon. We know r in terms of P and n, and also we know u (which is half of the perimeter) equals P/2. Substituting these values we get, A = (P / 2) * (P / (2n * tan(180/n))) A = P2 / (4n * tan(180/n)). |
*** (Back to Top)
|
Prove that the area of a
closed concave geometric figure equals the product of u (half of the perimeter of the
shape) and r (radius of the inscribed circle). (Assuming that an inscribed circle could be
drawn for the figure) ---- Let the figure be any polygon whose inscribed circle is also drawn. Let radius of the circle be r. If you connect O and the points at which the polygon is tangent to the circle, the lines that you draw will be perpendicular to the sides of the polygon and they will equal r in length (take |OH| as an example). So, if you calculate the areas of the triangles in the example, you get these: A(O A1 A2) = |A1A2| * r * 1/2 A(O A2 A3) = |A2A3| * r * 1/2 ... A(O A6 A7) = |A6A7| * r * 1/2 Sum of these areas will give the area of the polygon which, if you calculate, equals the product of half of the perimeter and radius of the inscribed circle. The proof doesn't depend on the number of the sides of the polygon. |
*** (Back to Top)
Interior angles of a triangle are proportional with 3, 4 and 7. What are its exterior angles proportional with respectively?
----
Let's say the interior angles are equal to 3k, 4k and 7k. Since sum of two interior angles is equal to the third angle's exterior, we can say that the exterior angles are equal to 11k, 10k and 7k. So, the exterior angles are proportional with 11, 10 and 7 respectively.
*** (Back to Top)
Interior angles of a quadrilateral are proportional with 3, 5, 8 and 9. What are its exterior angles proportional with respectively?
----
Let's say the interior angles are equal to 3k, 5k, 8k and 9k. In this case their total 25k equals 360 degrees. Using this, 12,5k equals 180 degrees. Then 3k's exterior angle equals 12,5k-3k=9,5k ; 5k's exterior angle equals 12,5k-5k=7,5k ; 8k's exterior angle equals 12,5k-8k=4,5k and 9k's exterior angle equals 12,5k-9k=3,5k. Multiplying each by two, we can conclude that the exterior angles are proportional with 19, 15, 9 and 7 respectively.
*** (Back to Top)
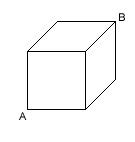 |
Suppose you are
a bug which wants to go from point A to point B walking on the cube. If one side of the
cube measures p units, how long is the shortest track in terms of p? ---- Suppose you lift the top face of the cube as shown in the figure. The shortest track connecting A and B' is a line which is also shown in the figure. After finding this, it is to calculate |AB'| with Pythgorean Theorem, which gives pÖ5. |
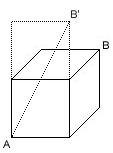 |